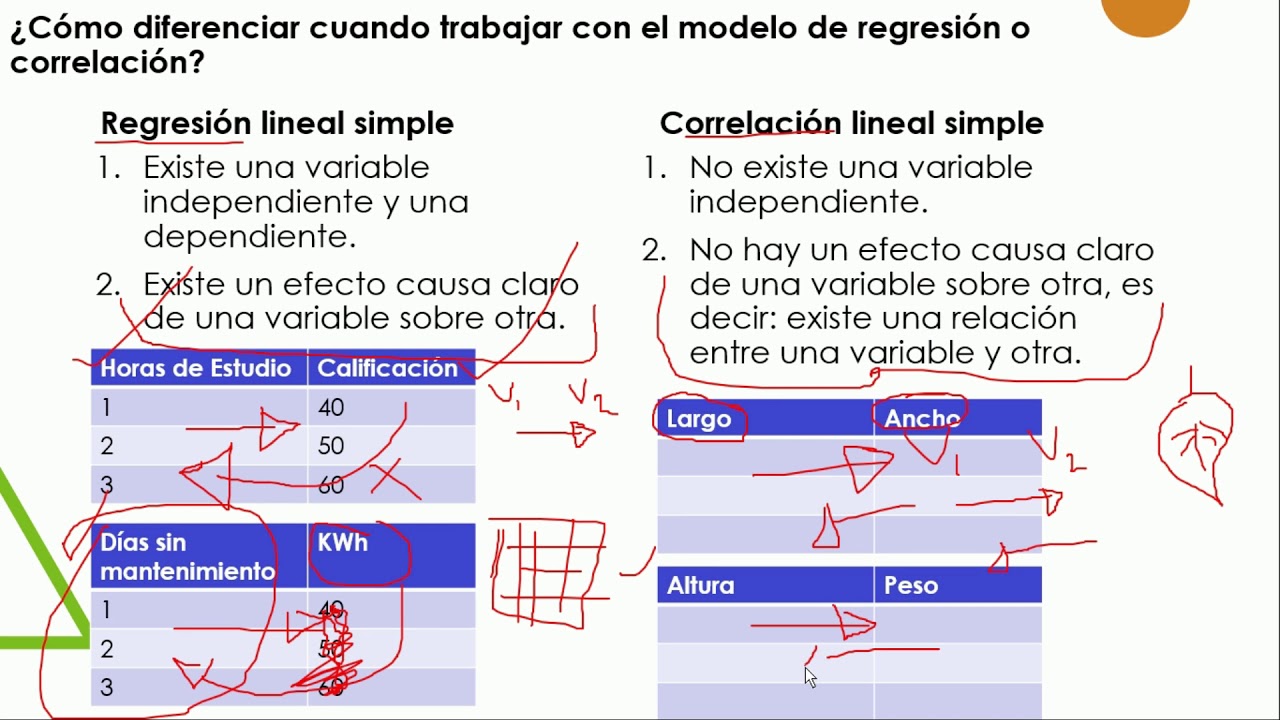
La correlación y la regresión son dos conceptos estadísticos que a menudo se confunden, pero que tienen significados y aplicaciones diferentes. Ambos son herramientas útiles para analizar relaciones entre variables, pero es importante entender sus diferencias para utilizarlos de manera efectiva. La correlación se refiere a la fuerza y dirección de una relación lineal entre dos variables, mientras que la regresión implica una relación más compleja, donde se busca predecir el valor de una variable basada en el valor de otra. A continuación, exploraremos en detalle cada uno de estos conceptos, sus características, sus usos y sus diferencias clave.
Definición de correlación
La correlación es una medida estadística que indica la extensión en la que dos variables están relacionadas. Se puede expresar mediante un coeficiente que varía entre -1 y 1. Un coeficiente de 1 indica una relación positiva perfecta, lo que significa que a medida que una variable aumenta, la otra también lo hace. Por otro lado, un coeficiente de -1 indica una relación negativa perfecta, donde el aumento de una variable se asocia con la disminución de la otra. Un coeficiente de 0 sugiere que no hay relación lineal entre las variables.
Existen diferentes tipos de correlación, siendo las más comunes la correlación de Pearson y la correlación de Spearman. La correlación de Pearson mide la relación lineal entre dos variables continuas y asume que ambas variables siguen una distribución normal. Por otro lado, la correlación de Spearman es una medida no paramétrica que se utiliza para variables ordinales o cuando no se cumplen los supuestos de normalidad. Es importante elegir el tipo de correlación adecuada según las características de los datos.
 Diferencia entre el ácido alfa lipoico y el ácido R lipoico
Diferencia entre el ácido alfa lipoico y el ácido R lipoicoDefinición de regresión
La regresión es un método estadístico utilizado para modelar la relación entre una variable dependiente y una o más variables independientes. A diferencia de la correlación, que solo mide la fuerza y dirección de la relación, la regresión permite predecir el valor de la variable dependiente basándose en los valores de las variables independientes. La forma más común de regresión es la regresión lineal, que busca encontrar la mejor línea recta que se ajuste a los datos.
La regresión lineal se expresa a través de una ecuación de la forma Y = a + bX, donde Y es la variable dependiente, X es la variable independiente, a es la intersección y b es la pendiente de la línea. Esta ecuación permite estimar el valor de Y para diferentes valores de X. Además de la regresión lineal, existen otros tipos de regresión, como la regresión múltiple, que incluye más de una variable independiente, y la regresión no lineal, que se utiliza cuando la relación entre las variables no es lineal.
Usos de la correlación
La correlación se utiliza en una variedad de campos, incluyendo la psicología, la economía, la biología y la investigación social. Uno de los usos más comunes es en la investigación para determinar si existe una relación entre dos variables. Por ejemplo, los investigadores pueden querer saber si hay una correlación entre el número de horas de estudio y las calificaciones de los estudiantes. Un análisis de correlación puede ayudar a identificar si los estudiantes que estudian más tienden a obtener mejores calificaciones.
 Diferencia entre el momento de enlace y el momento dipolar
Diferencia entre el momento de enlace y el momento dipolarOtro uso importante de la correlación es en la evaluación de la fiabilidad de las medidas. Por ejemplo, en psicología, se puede utilizar la correlación para evaluar si dos pruebas diferentes que miden el mismo constructo producen resultados similares. Si hay una alta correlación entre los resultados de las dos pruebas, se puede concluir que ambas son medidas confiables del mismo concepto.
- Investigación científica
- Evaluación de medidas
- Estudios de mercado
Usos de la regresión
La regresión se utiliza principalmente para hacer predicciones. Por ejemplo, las empresas pueden utilizar modelos de regresión para prever sus ventas futuras en función de variables como el precio, la publicidad y la economía. Esto permite a las empresas planificar mejor sus estrategias y tomar decisiones informadas. Además, la regresión se utiliza en la investigación para entender las relaciones causales entre variables. Por ejemplo, los economistas pueden utilizar la regresión para analizar cómo factores como la inflación y el desempleo afectan el crecimiento económico.
La regresión también es útil en el ámbito de la salud pública. Los investigadores pueden utilizar modelos de regresión para analizar cómo diferentes factores, como la dieta y el ejercicio, afectan la salud de una población. Esto puede ayudar a identificar intervenciones efectivas para mejorar la salud pública. la regresión es una herramienta poderosa para el análisis de datos y la toma de decisiones informadas.
 Diferencia entre género y especie
Diferencia entre género y especie- Predicción de ventas
- Análisis de relaciones causales
- Investigación en salud pública
Diferencias clave entre correlación y regresión
Una de las diferencias más importantes entre la correlación y la regresión es el tipo de información que proporcionan. La correlación se centra en medir la fuerza y dirección de una relación entre dos variables, mientras que la regresión se enfoca en la predicción y modelado de la relación. En otras palabras, la correlación responde a la pregunta de si dos variables están relacionadas, mientras que la regresión responde a la pregunta de cómo se relacionan y cómo se puede predecir una variable a partir de la otra.
Otra diferencia clave es el número de variables involucradas. La correlación generalmente se utiliza para analizar la relación entre dos variables, mientras que la regresión puede involucrar múltiples variables independientes. Esto significa que en un análisis de regresión, se pueden considerar varios factores que afectan la variable dependiente, lo que permite un análisis más completo y detallado.
Ejemplos de diferencias
- Correlación: Estudiar la relación entre el consumo de café y la productividad en el trabajo.
- Regresión: Predecir la productividad de un empleado basado en el consumo de café, horas de trabajo y nivel de estrés.
Además, es importante mencionar que la correlación no implica causalidad. Esto significa que, aunque dos variables estén correlacionadas, no se puede concluir que una causa la otra. Por ejemplo, puede haber una correlación entre el consumo de helado y el aumento de crímenes, pero esto no significa que comer helado cause delitos. La regresión, por otro lado, puede ayudar a identificar relaciones causales, siempre y cuando se utilicen adecuadamente los métodos y se consideren otras variables que puedan influir en la relación.
Interpretación de resultados
La interpretación de los resultados de la correlación y la regresión es fundamental para extraer conclusiones válidas. En el caso de la correlación, es importante considerar el coeficiente de correlación. Un valor cercano a 1 o -1 indica una fuerte relación, mientras que un valor cercano a 0 sugiere una relación débil. Sin embargo, también es crucial tener en cuenta el contexto de los datos y no apresurarse a sacar conclusiones sobre la causalidad.
En el caso de la regresión, la interpretación se basa en los coeficientes de la ecuación de regresión. Cada coeficiente indica cómo se espera que cambie la variable dependiente cuando la variable independiente aumenta en una unidad. Por ejemplo, si el coeficiente de la variable «horas de estudio» es 2 en un modelo de regresión que predice las calificaciones, esto significa que por cada hora adicional de estudio, se espera que la calificación aumente en 2 puntos. Además, es importante considerar el valor R cuadrado, que indica el porcentaje de variación en la variable dependiente que se explica por las variables independientes en el modelo.
Limitaciones de la correlación y regresión
Tanto la correlación como la regresión tienen sus limitaciones. En el caso de la correlación, una de las principales limitaciones es que no puede capturar relaciones no lineales. Si la relación entre las variables no es lineal, la correlación puede no ser una medida adecuada de la relación. Además, como se mencionó anteriormente, la correlación no implica causalidad, lo que puede llevar a interpretaciones erróneas si no se considera el contexto adecuado.
En cuanto a la regresión, una limitación importante es la necesidad de cumplir con ciertos supuestos. Por ejemplo, la regresión lineal asume que la relación entre las variables es lineal y que los errores son independientes y siguen una distribución normal. Si estos supuestos no se cumplen, los resultados de la regresión pueden ser engañosos. Además, si se incluyen demasiadas variables en un modelo de regresión, puede producirse un sobreajuste, lo que significa que el modelo se ajusta demasiado a los datos de entrenamiento y no generaliza bien a nuevos datos.
Aplicaciones prácticas de la correlación y regresión
Las aplicaciones prácticas de la correlación y regresión son diversas y abarcan muchos campos. En la economía, por ejemplo, se utilizan para analizar cómo diferentes factores, como el ingreso y la educación, afectan el consumo. Los economistas pueden usar la regresión para crear modelos que predigan el comportamiento del consumidor y ayudar a las empresas a tomar decisiones informadas sobre precios y marketing.
En el campo de la salud, la correlación y la regresión se utilizan para estudiar la relación entre factores de riesgo y enfermedades. Por ejemplo, los investigadores pueden analizar cómo el tabaquismo y la dieta afectan la incidencia de enfermedades cardíacas. Estos análisis son cruciales para la elaboración de políticas de salud pública y programas de prevención.
- Economía: Análisis de consumo y comportamiento del mercado.
- Salud: Estudio de factores de riesgo y enfermedades.
- Educación: Relación entre métodos de enseñanza y rendimiento estudiantil.
Conclusión sobre correlación y regresión
la correlación y la regresión son herramientas estadísticas valiosas, cada una con sus propias características y aplicaciones. La correlación se centra en la fuerza y dirección de la relación entre dos variables, mientras que la regresión permite predecir el valor de una variable basada en otra. Es fundamental comprender estas diferencias para utilizarlas de manera efectiva en el análisis de datos y la toma de decisiones. A través de ejemplos prácticos y una comprensión clara de sus limitaciones, podemos aplicar estos conceptos en diversas áreas y mejorar nuestra capacidad para analizar relaciones entre variables.